2015年05月09日  发布 version 1.0

好吧。我认为首先必须说，特征解实际上既给出了频率也给出了振型。特征解的数学过程可以按照不同的方式进行。对于解，有直接技术和间接技术之称。

对于较小的矩阵，直接技术对方程组进行分解，得到所有的特征值和特征向量。例如Jacobi、Givens和Householder变换技术是常用方法。

但是当矩阵变得更大时，诸如目前所通常开发的大型有限元模型，这时就利用间接技术，只得到一些低阶的模态。例如子空间迭代技术，同步向量迭代和Lacosz法是这些所用的间接技术中的几种。

但是，我实在不想将这篇文章搞成一堂数学课，或者陷到求解步骤的细枝末节中去。所以讨论一下特征解，以及求解频率和振型时，我们试图要怎么做？我要解释它，这样让你易于理解。

所以，我们按一般形式写出特征解。

[[K]-λ[m]]{x}={0}          (1)

首先我得说的是，特征值可以从矩阵的行列式中求得。嗯，实际上行列式只不过是一个高阶的多项式，其根为特征值。现在，从解析的角度看，它们可以根据任何的求根算法得到，例如，Secant法或者Newton-Rapson法，是几个熟知的方法。

因此，特征方程以及由此得到的典型多项式如图1所示。方程过零点处是根，此处多项式为零。

图1：行列式根的图形表示

现在，它给出了方程组的频率，下一步是确定模态振型。嗯，如果你取第1个特征值，λ=ω12，将它代入特征解的方程，则可以求得{x1}向量，因为[M]，[K]及ω12已知。用任何的分解方法解这个向量是简单而直接的，举几个熟知的常见方法，例如Crout-Doolittle，Cholesky，LDL分解。

因此，{x1}向量实际上就是那个用来解方程组的特定频率对应的模态振型。图2按图形方式展示了一个简支梁的第1阶自由-自由模态；注意，蓝色用来标识这是系统的第1阶模态。另外，如果你逐步观察图2中的方程，会发现按照它们所书写的方式，弹性力等于惯性力。我们也可以说这个量在ω1这个频率上是动态平衡的。同时，如果你从能量的角度来观察这个系统，可以理解为何有多个节点，在这里系统绕着这些点振荡，并且为了保持平衡，存在相同的正振型部分和负振型部分。

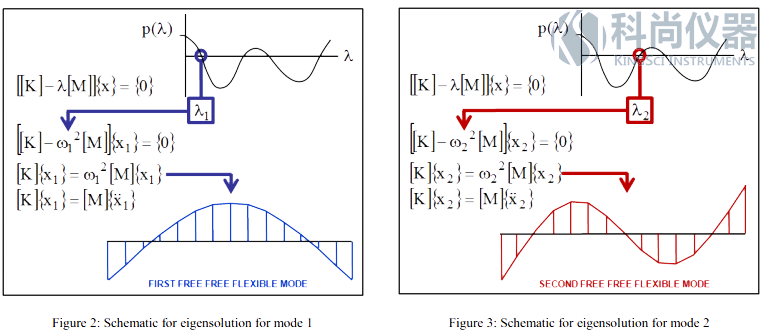
图2：1阶模态特征解的图示                                                                                   图3：2阶模态特征解的图示

自然了，现在对于第2个频率，我们需要做相同的事情。如果你取第2个特征值，λ=ω22，将它代入特征解的方程，则可以求得{x2}向量，因为[M]，[K]及ω22已知。现在{x2}向量实际上是第2个频率的模态振型。图3按照图形的方式展示了简支梁的第2阶自由-自由模态；注意，现在红色用来表示这是系统第2阶模态。再一次，我们逐步观察图3中红色的方程，你会注意到按照它们所书写的形式，弹性力等于惯性力。我们也可以讲，简支梁是动态平衡的，但是现在频率是ω22。跟我们对于1阶模态做过的那样，我们会明白节点是系统围绕着振荡的位置，并且为了保持平衡，振型有相等的正部分和负部分。

接下来，对于感兴趣的所有模态，我们可以继续这个过程。当然了，不同的求解算法实际上分解矩阵和得到最终解的方法可能跟我解释它的方法不一样。但是，我解释它的方法也许会让你对于频率和模态振型是如何从系统方程组中得到的，有一个更好的总体把握。

因此重要的是特征解用来得到所谓的特征对偶 – 也即，频率以及与特征方程相关联的向量。实际上这就是模态振型。

现在，要认识的另外一件事情是，模态振型是线性独立的，同时模态振型关于质量和刚度矩阵也是正交的。这是一个非常重要的事实，用测得的试验数据来检验有限元模型时，我们常用它。我们进行一种正交检验，常被称为伪正交检验，来对测得的试验向量和从特征解得到的向量进行对比。

我希望这有助于解释你的问题。如果你有关于模态分析的任何其他问题，尽管问我好了。

返回模态空间中文翻译目录